Z. Ye, O. Diamanti, C. Tang, L.J. Guibas, T. Hoffmann, A unified discrete framework for intrinsic and extrinsic Dirac operators for geometry processing, Comput. Graph. Forum 37(5): 93-106(2018).

Abstract:

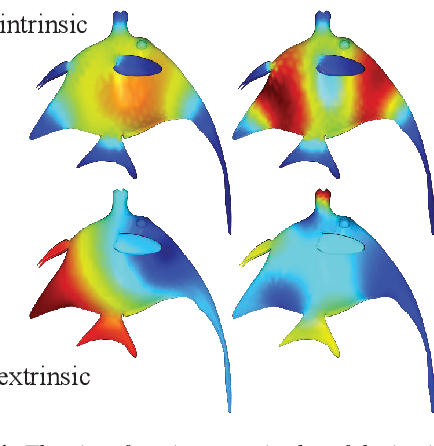
Spectral mesh analysis and processing methods, namely ones that utilize eigenvalues and eigenfunctions of linear operators on meshes, have been applied to numerous geometric processing applications. The operator used predominantly in these methods is the Laplace-Beltrami operator, which has the often-cited property that it is intrinsic, namely invariant to isometric deformation of the underlying geometry, including rigid transformations. Depending on the application, this can be either an advantage or a drawback. Recent work has proposed the alternative of using the Dirac operator on surfaces for spectral processing. The available versions of the Dirac operator either only focus on the extrinsic version, or introduce a range of mixed operators on a spectrum between fully extrinsic Dirac operator and intrinsic Laplace operator. In this work, we introduce a unified discretization scheme that describes both an extrinsic and intrinsic Dirac operator on meshes, based on their continuous counterparts on smooth manifolds. In this discretization, both operators are very closely related, and preserve their key properties from the smooth case. We showcase various applications of our operators, with improved numerics over prior work

Bibtex: 

@article{ydtgh-audffiaedofgp-18,
  title={A unified discrete framework for intrinsic and extrinsic Dirac operators for geometry processing},
  author={Zi Ye and Olga Diamanti and Chengcheng Tang and Leonidas J. Guibas and Tim Hoffmann},
  journal={Comput. Graph. Forum},
  year={2018},
  volume={37},
  pages={93-106}
}